- Published on
Stacks built with Typescript for portuguese speakers
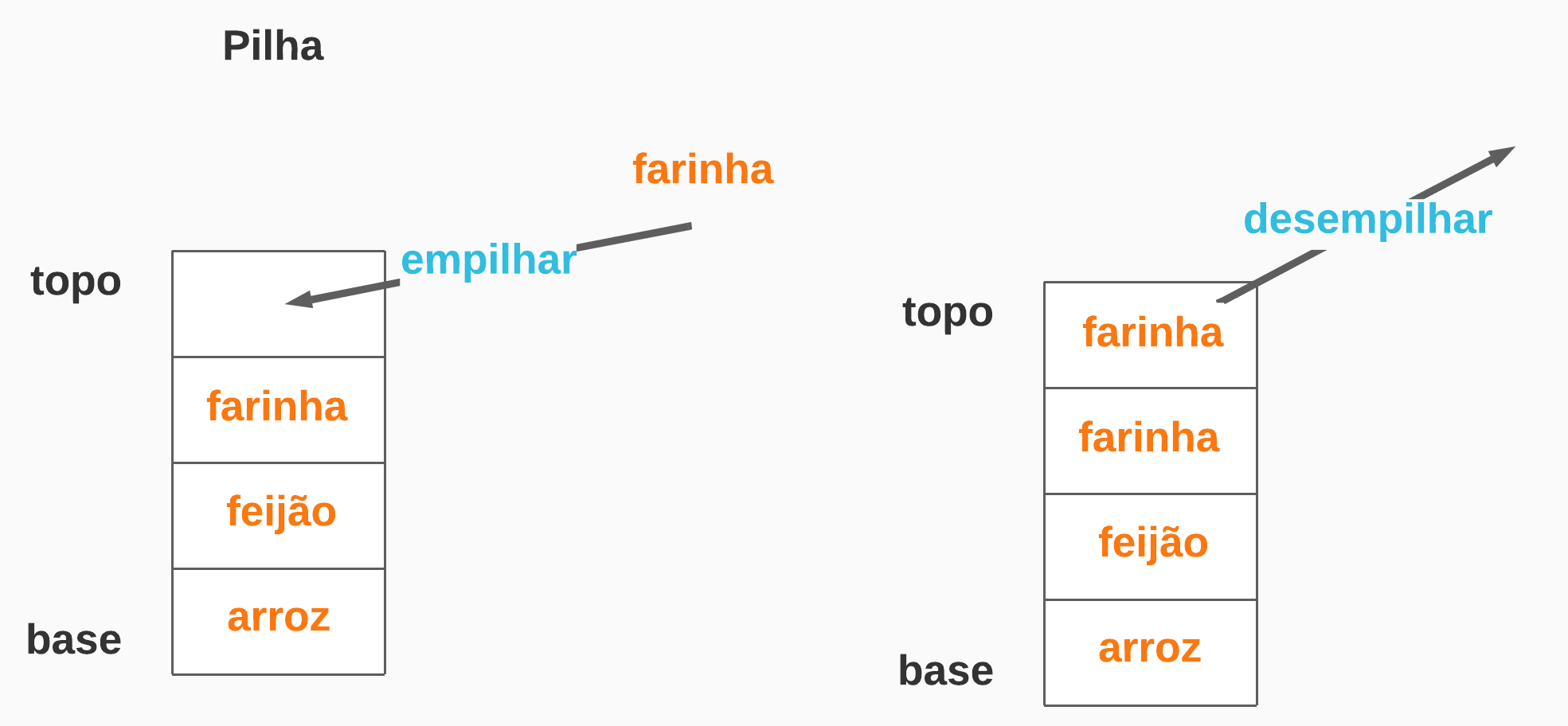
Pilhas - Stacks
Pilhas são estruturas de dados que suportam operações de adição e remoção de elementos e obrigatoriamente deve implementar as seguintes regras:
- A adição de novos elementos é feita no topo da estrutura.
- Na remoção, o elemento removido é o que está na estrutura há menos tempo. Ou seja, o elemento removido é que se encontra no topo.
Dessa forma, podemos dizer que o primeiro objeto a ser inserido na pilha é o último a ser removido.
Esse padrão é conhecido pela sigla LIFO, que significa Last-In-First-Out.
Complexidade de tempo e espaço - Big O
Independentemente do tamanho N da pilha, numa pilha ideal, operações básicas devem ocorrer em O(1) - tempo constante considerando a memória já alocada. A complexidade será O(n) quando a memória alocada for excedida em operações de inserção.
Pilha.empilhar
Complexidade de tempo: O(1)
Complexidade de espaço: O(1)
Pilha.desempilhar
Complexidade de tempo: O(1)
Complexidade de espaço: O(1)
Pilha.itemNoTopo
Complexidade de tempo: O(1)
Complexidade de espaço: O(1)
Implementação em um vetor
Suponha que nossa pilha está armazenada em um vetor, onde N é o capacidade ou comprimento máximo da pilha:
pilha[0..N-1]
O tipo de dados dos elementos do vetor é irrelevante.
Digamos que a parte do vetor ocupada pela pilha é:
pilha[0..t-1]
O índice t indica a primeira posição vaga do vetor e t-1 é o índice do topo da pilha.
A pilha está vazia se t vale 0 e cheia se t vale N.
No exemplo á seguir, os caracteres A, B, … , H foram inseridos na pilha nessa ordem:

Conceitualmente, para desempilhar (remover) um elemento da pilha, faça:
t -= 1;
x = pilha[t];
Não é possível desempilhar em uma pilha vazia.
Conceitualmente, para empilhar (inserir) um ítem y na pilha, faça:
pilha[t] = y;
t += 1;
Caso a pilha esteja cheia e haja a tentativa de um empilhamento deve ocorrer um transbordamento. Do inglês: overflow, ou, stack oveflow.
Implementação de uma Pilha usando a linguagem Typescript.
Posição no vetor
O principal requerimento funcional da pilha é:
primeiro objeto a ser inserido na pilha é o último a ser removido.
Com isso fica aberta a possibilidade de usar o início do vetor como topo e o final como base da pilha. Darei o nome á essa implementação de Pilha inversa e que possui tempo de O(n) no pior cenário, pois ao remover o primeiro item do vetor, o mesmo é completamente redimensionado.
topo = Pilha[0]
base = Pilha[Pilha.length - 1]
Porém, na implementação á seguir, o final do vetor será o topo e o começo será a base da pilha.
topo = Pilha[Pilha.length - 1]
base = Pilha[0]
Implementarei o algorítimo da pilha dessa forma visando uma maior performance. Em Javascript, ao lidar com vetores contendo muitos ítens, é mais custoso manipular os primeiros elementos do que os últimos.
Capacidade da Pilha
Vetores em javascript se comportam um pouco diferente do que em outras linguagens. a Pilha poderia ser criaada associando um tamanho ao array, pilha = new Array(10), mas isso criaria um vetor com 10 slots vazios e não um vetor com 10 slots com valores indefinidos. Logo criaremos um vetor com tamanho dinâmico e usaremos uma variável auxiliar para emular a capacidade máxima da pilha.
Tipo da pilha
Apesar do tipo de dados dos elementos do vetor ser irrelevante, a implementação á seguir associa um tipo de dado específico aos ítems do vetor.
Vamos ao código
export class Pilha <T> {
/**
* vetor para armazenar os dados da pilha
*/
private pilha: Array<T> = [];
/**
* em Typescript/Javascript não há arrays com dimensão fixa.
* essa proriedade será usada para emular a capacidade máxima
* de armazenamento da pilha.
*/
private _capacidade: number;
/**
* O construtor da pilha suportará um objeto como parâmetro, contendo 2 atributos opcionais:
* capacidade: define a capacidade máxima de armazenamento da pilha. Padrão: 10
* valores: elementos que serão inseridos ao criar a pilha. Padrão: nenhum
*/
constructor(
{ capacidade, valores }: { capacidade?: number, valores?: T[] }
)
{
this._capacidade = capacidade ? capacidade : 10;
if (valores) {
for (let x = 0; x < (valores?.length || 0); x++) {
const valor = valores[x];
this.empilhar(valor);
}
}
}
// empilhar item no topo da pilha
public empilhar(valor: T): Array<T> {
if (this.tamanho === this.capacidade) {
throw new Error('Pilha transbordada - Stack overflow')
}
// O(1)
this.pilha.push(valor);
return this.pilha;
}
// tirar o último ítem da lista
public desempilhar (): T {
if (!(this.pilha.length > 0)) {
throw new Error('Pilha vazia');
}
// O(1)
return this.pilha.pop() as unknown as T;
}
// checa se pilha está vazia
public get estaVazia (): boolean {
return !!(this.pilha.length === 0);
}
// recupera o ítem na base da pilha
public get base () {
return this.pilha[0];
}
// recupera o ítem no topo da pilha
public get itemNoTopo () {
return this.pilha[this.topo];
}
// recupera o index do topo
public get topo () {
return this.pilha.length - 1;
}
// retorna o tamanho da pilha
public get tamanho() {
return this.pilha.length;
}
public get capacidade() {
return this._capacidade;
}
}
Uso
const valores = ['arroz', 'feijão', 'farinha'];
const pilha = new Pilha<string>({ valores, capacidade: 30 }); // ou new Pilha({ valores })
while (pilha.tamanho < pilha.capacidade) {
pilha.empilhar('açúcar');
}
Solução de Problemas
Balanceamento de parênteses
A capacidade de diferenciar entre sequências de parênteses corretamente balanceadas daquelas que estão desbalanceadas é um componente importante no reconhecimento estruturas em muitas linguagens de programação.
O desafio então é escrever um algoritmo que leia uma string de parênteses da esquerda para a direita e decida se os parênteses estão balanceados. Para resolver este problema, precisamos fazer uma observação importante. Ao examinar da esquerda para a direita os símbolos na string, cada fecha parêntese deve ser associado ao abre parêntese que foi examinado mais recentemente e ainda não foi associado a um fecha parêntese. Além disso, o primeiro abre parêntese examinado pode ter que esperar até o último símbolo da string para encontrar o seu fecha parêntese. Fecha parênteses são associados a abre parênteses na ordem inversa que foram examinados; eles são emparelhados de “dentro para fora”. Este é um indício de que pilhas podem ser usadas para resolver problema.
São considerados os elementos de abertura: { [ ( <
São considerados os elementos de fechamento: } ] ) >
function taBalanceado(caracteres: string | string[]): boolean {
// criar pilha vazia
const pilha: Pilha<string> = new Pilha({ capacidade: 500 });
for (const bracket of caracteres) {
if (bracket === '[') {
pilha.empilhar(bracket);
} else if (bracket === '{') {
pilha.empilhar(bracket);
} else if (bracket === '<') {
pilha.empilhar(bracket);
} else if (bracket === '(') {
pilha.empilhar(bracket);
} else if (bracket === ']') {
if (pilha.itemNoTopo === '[') {
pilha.desempilhar();
} else {
pilha.empilhar(bracket);
}
} else if (bracket === '}') {
if (pilha.itemNoTopo === '{') {
pilha.desempilhar();
} else {
pilha.empilhar(bracket);
}
} else if (bracket === '>') {
if (pilha.itemNoTopo === '<') {
pilha.desempilhar();
} else {
pilha.empilhar(bracket);
}
} else if (bracket === ')') {
if (pilha.itemNoTopo === '(') {
pilha.desempilhar();
} else {
pilha.empilhar(bracket);
}
} else {
continue;
}
}
return pilha.tamanho === 0;
}
Testes
it('a string ([]) deve tá balanceada', () => {
expect(taBalanceado('([])'.split(''))).toBeTruthy();
});
it('a string {} deve tá balanceada', () => {
expect(taBalanceado('{}'.split(''))).toBeTruthy();
});
it('a string ([][]) deve tá balanceada', () => {
expect(taBalanceado('([][])'.split(''))).toBeTruthy();
});
it('a string ([][]<>)() deve tá balanceada', () => {
expect(taBalanceado('([][]<>)()'.split(''))).toBeTruthy();
});
it('a string ([][]<>)(abc) deve tá balanceada', () => {
expect(taBalanceado('([][]<>)(abc)'.split(''))).toBeTruthy();
});
it('a string ((((((((((([][]<>)(abc))))))))))) deve tá balanceada', () => {
expect(taBalanceado('((((((((((([][]<>)(abc)))))))))))'.split(''))).toBeTruthy();
});
it('a string ([>]) não deve tá balanceado', () => {
expect(taBalanceado('([>])'.split(''))).toBeFalsy();
});
it('a string ([]>) não deve tá balanceado', () => {
expect(taBalanceado('([]>)'.split(''))).toBeFalsy();
});
it('a string {}} não deve tá balanceado', () => {
expect(taBalanceado('{}}'.split(''))).toBeFalsy();
});
Benchmark
Hardware
Mac Mini
Processor: 3 GHz 6-Core Intel Core i5
Memory: 32 GB 2667 MHz DDR4
Requerimento
Considerando a idéia de Pilha e Pilha inversa citada anteriormente. Veja a seguir o benchmark para cada tipo de implementação:
O programa deverá criar uma Pilha contendo os ítens 'arroz', 'feijão', 'farinha' e com capacidade de 100.000 ítens.
Após a pilha ser criada, o programa deverá empilhar novos ítens até atingir a capacidade máxima da pilha.
const valores = ['arroz', 'feijão', 'farinha'];
const pilha = new Pilha<string>({ valores, capacidade: 100000 }); // ou new Pilha({ valores })
while (pilha.tamanho < pilha.capacidade) {
pilha.empilhar('açúcar');
}
Resultados
Pilha- 100.000 ítens
$ ts-node ./src/Pilhas/benchmark/pilha.ts
Tempo de execução: 5.504647 ms
consumo aproximado: 100.20630645751953 MB
Pilha inversa- 100.000 ítens
ts-node ./src/Pilhas/benchmark/pilha_inversa.ts
Tempo de execução: 928.442721 ms
consumo aproximado: 100.38533782958984 MB
Pilha- 500.000 ítens
$ ts-node ./src/Pilhas/benchmark/pilha.ts
Tempo de execução: 12.728368 ms
consumo aproximado: 111.29053497314453 MB
Pilha inversa- 500.000 ítens
ts-node ./src/Pilhas/benchmark/pilha_inversa.ts
Tempo de execução: 25577.447571 ms
consumo aproximado: 111.19620513916016 MB
Repositório
O código completo poderá ser encontrado em https://github.com/web2solutions/ds-ts/tree/main/src/Pilhas.
Todos os arquivos para download: https://github.com/web2solutions/ds-ts/raw/main/src/Pilhas.zip